[toc]

动态规划算法

1. 应用场景-背包问题

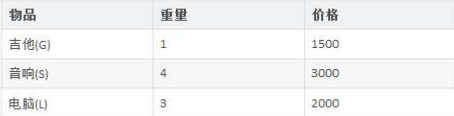
背包问题：有一个背包，容量为 4 磅 ， 现有如下物品

image-20200907182914989

  1. 要求达到的目标为装入的背包的总价值最大，并且重量不超出
  2. 要求装入的物品不能重复

2. 动态规划算法介绍

  1. 动态规划(Dynamic Programming)算法的核心思想是：将 大问题划分为小问题进行解决，从而一步步获取最优解的处理算法。
  2. 动态规划算法与分治算法类似，其基本思想也是将待求解问题分解成若干个子问题，先求解子问题，然后从这些子问题的解得到原问题的解。
  3. 与分治法不同的是，适合于用动态规划求解的问题，经分解得到子问题往往不是互相独立的。 ( 即下一个子阶段的求解是建立在上一个子阶段的解的基础上，进行进一步的求解 )
  4. 动态规划可以通过填表的方式来逐步推进，得到最优解。

3. 动态规划算法最佳实践-背包问题

3.1 思路分析和图解

  1. 背包问题主要是指一个给定容量的背包、若干具有一定价值和重量的物品，如何选择物品放入背包使物品的价值最大。其中又分 01 背包和 完全背包(完全背包指的是：每种物品都有无限件可用)

  2. 这里的问题属于 01 背包，即每个物品最多放一个。而无限背包可以转化为 01 背包。

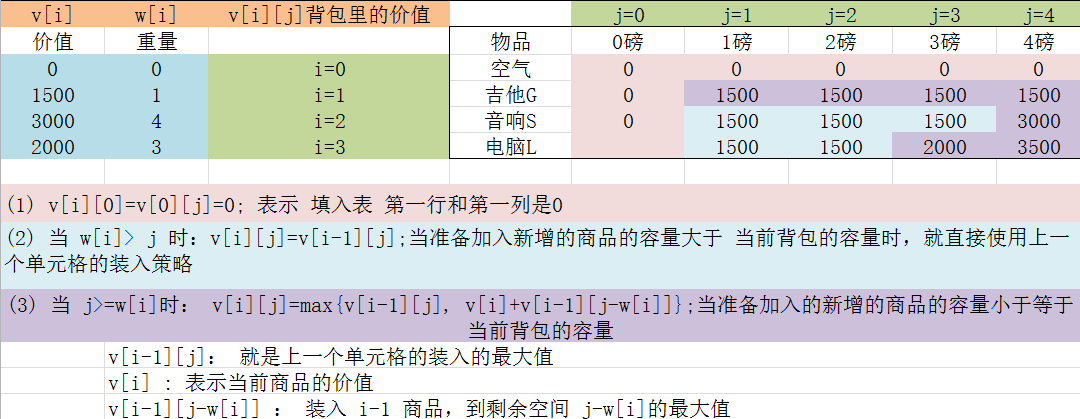
  3. 算法的主要思想，利用动态规划来解决。每次遍历到的第 i 个物品，根据 w[i]和 v[i]来确定是否需要将该物品放入背包中。即对于给定的 n 个物品，设 v[i]、w[i]分别为第 i 个物品的价值和重量，j为背包的容量。再令 v[i][j]表示在前 i 个物品中能够装入容量为 j 的背包中的最大价值。则我们有下面的结果：

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    // 表示 填入表 第一行和第一列是 0
    (1) v[i][0]=v[0][j]=0; 

    // 当准备加入新增的商品的容量大于 当前背包的容量时，就直接使用上一个单元格的装入策略
    (2) 当 w[i]> j 时：v[i][j]=v[i-1][j] 
        
    // 当 准备加入的新增的商品的容量小于等于当前背包的容量,
    (3) 当 j>=w[i]时： v[i][j]=max{v[i-1][j], v[i]+v[i-1][j-w[i]]}
        // 装入的方式:
        v[i-1][j]： 就是上一个单元格的装入的最大值
        v[i] : 表示当前商品的价值
        v[i-1][j-w[i]] ： 装入 i-1 商品，到剩余空间 j-w[i]的最大值

  4. 如果上面的看不懂，请仔细看下图：

  5. image-20201010101815093

3.2 代码实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
package cn.itbuild.dynamic;

public class KnapsackProblem {

	public static void main(String[] args) {
		// 物品的重量
		int[] w = {1,4,3};
		// 物品的价值, 这里 val[i] 就是前面讲的 v[i]
		int[] val = {1500,3000,2000};
		
		// 背包的容量，遍历的时候用j表示
		int m = 4;
		// 物品的数量，遍历的时候用i表示
		int n = val.length;
		
		// v[i][j] 表示在前 i个物品中能够装入容量为 j的背包中的`最大价值`
		// 为什么+1呢？因为第一行和第一列都要置为零
		int[][] v = new int[n+1][m+1];
		
		// 初始化第一行和第一列，这里在本程序中，可以不去处理，因为默认就是 0
		// 第一列置为零
		for (int i = 0; i < v.length; i++) {
			v[i][0] = 0;
		}
		
		// 第一行置为零
		for (int i = 0; i < v[0].length; i++) {
			v[0][i] = 0;
		}
		
		// 核心逻辑
		// 根据前面得到公式来动态规划处理
		for (int i = 1; i < v.length; i++) {
			// 背包容量
			for (int j = 1; j < v[0].length; j++) {
				
				// 因为i是从1开始的所以要减一
				// 如果背包剩余的容量小于当前物品的容量，执行以下内容：
				if(w[i-1] > j) {
				
					v[i][j] = v[i-1][j];
			
				// 否则：即是w[i-1] <= j
				}else {	
					v[i][j] = Math.max(v[i-1][j], val[i-1] + v[i-1][j-w[i-1]]);
				}
				
			}
		}
		// 输出最能放入的最大价值
		System.out.println(v[n][m]);// 3500
	}

}

可以求出放入背包的最大价值，但是不能求出背包里面的都是放的什么物品，所以我们通过下面进行改进。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
package cn.itbuild.dynamic;

public class KnapsackProblem {

	public static void main(String[] args) {
		// 物品的重量
		int[] w = {1,4,3};
		// 物品的价值, 这里 val[i] 就是前面讲的 v[i]
		int[] val = {1500,3000,2000};
		
		// 背包的容量，遍历的时候用j表示
		int m = 4;
		// 物品的数量，遍历的时候用i表示
		int n = val.length;
		
		// v[i][j] 表示在前 i个物品中能够装入容量为 j的背包中的`最大价值`
		// 为什么+1呢？因为第一行和第一列都要置为零
		int[][] v = new int[n+1][m+1];
		
		// 为了记录放入商品的情况，我们定一个二维数组
		int[][] path = new int[n+1][m+1];
		
		// 初始化第一行和第一列，这里在本程序中，可以不去处理，因为默认就是 0
		// 第一列置为零
		for (int i = 0; i < v.length; i++) {
			v[i][0] = 0;
		}
		
		// 第一行置为零
		for (int i = 0; i < v[0].length; i++) {
			v[0][i] = 0;
		}
		
		// 核心逻辑
		// 根据前面得到公式来动态规划处理
		for (int i = 1; i < v.length; i++) {
			// 背包容量
			for (int j = 1; j < v[0].length; j++) {
				
				// 因为i是从1开始的所以要减一
				// 如果背包剩余的容量小于当前物品的容量，执行以下内容：
				if(w[i-1] > j) {
				
					v[i][j] = v[i-1][j];
			
				// 否则：即是w[i-1] <= j
				}else {	
					// v[i][j] = Math.max(v[i-1][j], val[i-1] + v[i-1][j-w[i-1]]);
					// 再通过一次if else把放进入的物品进行记录
					if (v[i-1][j] < val[i-1] + v[i-1][j-w[i-1]]) {
						v[i][j] = val[i-1] + v[i-1][j-w[i-1]];
						path[i][j] = 1;
					}else {
						v[i][j] = v[i-1][j];
					}
					
				}
				
			}
		}	
		
		// 输出一下 v 看看情况
		for(int i =0; i < v.length;i++) {
			for(int j = 0; j < v[i].length;j++) {
				System.out.print(v[i][j] + " ");
			}
			System.out.println();
		}
		
		System.out.println("***********************");
		
		// 行的最大下标
		int i = path.length - 1;
		// 列的额最大下标
		int j = path[0].length -1;
		// 从path的最后面开始找
		while(i>0 && j>0) {
			if (path[i][j] == 1) {
				System.out.printf("第 %d 个商品放入到背包\n", i);
				// 背包重量需要减去当前物品的重量
				j = j - w[i-1];
			}
			i--;
		}
		
	}
}

结果：

1
2
3
4
5
6
7
8
9
0 0 0 0 0 
0 1500 1500 1500 1500 
0 1500 1500 1500 3000 
0 1500 1500 2000 3500 

***********************

第 3 个商品放入到背包
第 1 个商品放入到背包

☆