[toc]

二叉排序树

给你一个数列 (7, 3, 10, 12, 5, 1, 9)，要求能够高效的完成对数据的查询和添加

  • 使用数组

    数组未排序:

    • 优点：直接在数组尾添加，速度快。

    • 缺点：查找速度慢.

    数组排序:

    • 优点：可以使用二分查找，查找速度快
    • 缺点：为了保证数组有序，在添加新数据时，找到插入位置后，后面的数据需整体移动，速度慢。

  • 使用链式存储-链表

    不管链表是否有序，查找速度都慢，添加数据速度比数组快，不需要数据整体移动

  • 使用二叉排序树

1. 二叉排序树介绍

  1. 二叉排序树：**BST: (Binary Sort(Search) Tree)**, 对于二叉排序树的 任何一个非叶子节点，要求 左子节点的值比当前节点的值小， 右子节点的值比当前节点的值大。
  2. 特别说明：如果有相同的值，可以将该节点放在左子节点或右子节点
  3. 比如针对前面的数据 (7, 3, 10, 12, 5, 1, 9) ，对应的二叉排序树为

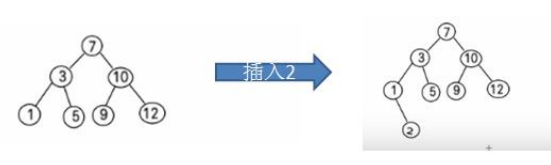
image-20200323184213984

2. 二叉排序树的创建

2.1 节点Node创建

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
/**
 * 创建Node节点
 * @author DuanChaojie
 * @date 2020年3月23日 上午11:13:35
 * @version 1.0
 */
class Node{
	
	int value;
	
	Node left;
	
	Node right;

	//构造器
	public Node(int value) {
		this.value = value;
	}

	//toString方法
	@Override
	public String toString() {
		return "Node [value=" + value + "]";
	}
	
	
	/**
	 * 添加基地那的方法
	 * 递归的形式添加节点，注意满足二叉排序树的需求
	 * @param node
	 */
	public void add(Node node) {
		
		if(node == null) {
			return;
		}
		
		//判断传入的节点的值，和当前子树的根节点的值得关系
		if(node.value < this.value) {
			//如果当前节点左子节点为null
			if(this.left == null) {
				this.left = node;
			}else {
				//递归向左子树添加
				this.left.add(node);
			}
		//添加的节点的值大于等于当前节点的值
		}else {
			if(this.right == null) {
				this.right = node;
			}else {
				//递归向右子树添加
				this.right.add(node);
			}
			
		}
	}
	
	/**
	 * 中序遍历BST
	 */
	public void infixOrder() {
		
		if(this.left != null) {
			this.left.infixOrder();
		}
		
		System.out.println(this);
		
		if(this.right != null) {
			this.right.infixOrder();
		}
	}
		
}

2.2 BST二叉排序树的创建

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
/**
 * 创建二叉排序树 BST
 * @author DuanChaojie
 * @date 2020年3月23日 上午11:32:49
 * @version 1.0
 */
class BinarySortTree{
	
	private Node root;
	
	
	//getter和setter方法
	public Node getRoot() {
		return root;
	}



	public void setRoot(Node root) {
		this.root = root;
	}



	/**
	 * 添加节点的方法
	 * @param node
	 */
	public void add(Node node) {
		
		if(root == null) {
			//如果root为null，直接让root指向node
			root = node;
		}else {
			root.add(node);
		}
	}
	
	/**
	 * 中序遍历的方法
	 */
	public void infixOrder() {
		if(root != null) {
			root.infixOrder();
		}else {
			System.out.println("二叉排序树为空不能遍历");
		}
	}
	
}

2.3 测试并创建的顺序二叉树

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
public class BinarySortTreeDemo {

	public static void main(String[] args) {

		int[] arr = {7,3,10,12,5,1,9,2};
		BinarySortTree binarySortTree = new BinarySortTree();
		
		//循环添加节点到二叉排序树
		for (int i = 0; i < arr.length; i++) {
			
			binarySortTree.add(new Node(arr[i]));
			
		}
		
		System.out.println("中序遍历二叉排序树");
		binarySortTree.infixOrder();
    }
}

3. 二叉排序树的删除

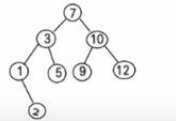
二叉排序树的删除情况比较复杂，有下面三种情况需要考虑：

  1. 删除叶子节点 (比如：2, 5, 9, 12)
  2. 删除点 只有一颗子树的节点 (比如：1)
  3. 删除 有两颗子树的节点. (比如：7, 3，10 )
  4. image-20200323185546112
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
//对删除结点的各种情况的思路分析:


第一种情况:删除叶子节点 (比如：2, 5, 9, 12)
	思路:
    (1) 需求先去找到要删除的结点 targetNode
    (2) 找到 targetNode 的 父结点 parent
    (3) 确定 targetNode 是 parent 的左子结点 还是右子结点
    (4) 根据前面的情况来对应删除	
        左子结点 parent.left = null
        右子结点 parent.right = null;


第二种情况: 删除只有一颗子树的节点 比如 1
	思路:
    (1) 需求先去找到要删除的结点 targetNode
    (2) 找到 targetNode 的 父结点 parent
    (3) 确定 targetNode 的子结点是左子结点还是右子结点
    (4) targetNode 是 parent 的左子结点还是右子结点
    (5) 如果 targetNode 有左子结点
    	5.1 如果 targetNode 是 parent 的左子结点 parent.left = targetNode.left;
    	5.2 如果 targetNode 是 parent 的右子结点 parent.right = targetNode.left;
    (6) 如果 targetNode 有右子结点
    	6.1 如果 targetNode 是 parent 的左子结点 parent.left = targetNode.right;
    	6.2 如果 targetNode 是 parent 的右子结点 parent.right = targetNode.right
            
第三种情况: 删除有两颗子树的节点. (比如：7, 3，10 ) 思路:
    (1) 需求先去找到要删除的结点 targetNode
    (2) 找到 targetNode 的 父结点 parent
    (3) 从 targetNode 的右子树找到最小的结点
    (4) 用一个临时变量，将 最小结点的值保存 temp = 11
    (5) 删除该最小结点
    (6) targetNode.value = temp

3.1 Node类中添加以下方法

  • public Node search(int value);
  • public Node searchParent(int value);
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
/**
 * 
 * @param value 希望删除的节点的值
 * @return 如果找到返回该节点，否则返回为null
 */
public Node search(int value) {
	
	// 找到就是该节点
	if(value == this.value) {
		return this;
           
	// 如果查找的值小于当前节点，向左子树递归查找
	}else if(value < this.value) {
		
		//如果左子树为空
		if(this.left == null) {
			return null;
		}
		return this.left.search(value);
		
		//如果查找的值不小于当前节点，向右子树递归查找
	}else {
		
		if(this.right == null) {
			return null;
		}	
		return this.right.search(value);	
	}	
}

/**
 * @param value 要找到的值得节点
 * @return 返回的是要删除的节点的父节点，如果没有就返回null
 */
public Node searchParent(int value) {
	
	//如果当前节点就是要删除的节点的父节点，就返回
	if((this.left != null && this.left.value == value)|| (this.right != null && this.right.value == value)) {
		return this;
	}else  {
		
		//如果查找的值小于当前节点的值，并且当前节点的左子节点不为空
		if(value < this.value && this.left != null) {
			return this.left.searchParent(value);
		}else if(value >= this.value && this.right != null) {
			return this.right.searchParent(value);
		}else {
			return null;
		}
	}	
       
}

3.2 BinarySortTree类中添加以下方法

  • public Node search(int value)；
  • public Node searchParent(int value)；
  • public void delNode(int value)；
  • public int delRightTreeMin(Node node)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
/*
 * 寻找节点的方法
 */
public Node search(int value) {
	//如果根节点为空，则直接返回为null
	if(root == null) {
		return null;
	}else {
		return root.search(value);
	}
}

/**
 * 寻找父节点
 * @param value
 * @return
 */
public Node searchParent(int value) {
	if(root == null) {
		return null;
	}else {
		return root.searchParent(value);
	}
}

/**
 * 删除二叉排序树的方法
 * @param value 要删除节点的值
 */
public void delNode(int value) {
	if(root == null) {
		return;
	}else {
		//1.需要先去找到要删除的节点 targetNode
		Node targetNode = search(value);
		
		//2.如果没有找到要删除的节点
		if(targetNode == null) {
			return;
		}
		
		//如果我们发现当前二叉树只有一个节点
		if(root.left == null && root.right == null) {
			root = null;
			return;
		}
		
		//去找targetNode的父节点
		Node parentNode = searchParent(value);
		
		
		//如果要删除的是叶子节点
		if(targetNode.left == null && targetNode.right == null ) {
			
			//判断是父节点的左子节点还是右子节点
			if(parentNode.left != null && parentNode.left.value == value) {
				//如果是父节点的左子节点
				parentNode.left = null;
			}else if(parentNode.right != null && parentNode.right.value == value) {
				//如果是父节点的右子节点
				parentNode.right = null;
			}
			
			//
		}else if(targetNode.left != null && targetNode.right != null) {
			int minVal = delRightTreeMin(targetNode.right);
			targetNode.value = minVal;

			//删除的只有一课子树的节点
		}else {
			//如果删除的节点有左子节点
			if(targetNode.left != null) {
				
				if(parentNode != null) {
					//如果targetNode 是parentNode的左子节点
					if(parentNode.left.value == value) {
						parentNode.left = targetNode.left;
					}else {
						parentNode.right = targetNode.left;
					}
				}else {
					root = targetNode.left;
				}
			//如果要删除的节点有右子节点	
			}else {
				if(parentNode != null) {
					if(parentNode.left.value == value) {
						parentNode.left = targetNode.right;
					}else {
						parentNode.right = targetNode.right;
					}
				}else {
					root = targetNode.right;
				}
			}
		}
	// 第一个else
	}
// 方法的结尾	
}

/**
 * 1. 返回的以Node为根节点的二叉排序树的最小节点的值
 * 2. 删除node为根节点的二叉排序树的最小节点
 * @param node
 * @return
 */
public int delRightTreeMin(Node node) {
	
	Node target = node;
	
	//循环查找左子节点，就会找到最小值
	while(target.left != null) {
		target = target.left;
	}
	
	// 这时候target就指向最小的节点
       // 删除最小结点
	delNode(target.value);
	return target.value;
}

☆