1. 排序算法的介绍

排序也称排序算法(SortAlgorithm)，排序是将 一组数据，依 指定的顺序进行 排列的过程。

1.2 排序的分类

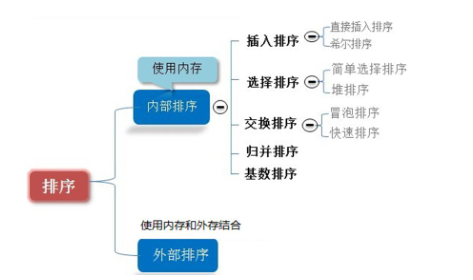
  1. 内部排序:
    指将需要处理的所有数据都加载到 内部存储器( 内存) 中进行排序。
  2. 外部排序法：
    数据量过大，无法全部加载到内存中，需要借助 外部存储(文件等)进行排序。

1.2.1 常见的排序算法分类

1.3 算法的时间复杂度

1.3.1 度量一个程序(算法)执行时间的两种方法

  1. 事后统计的方法
    这种方法可行, 但是有两个问题：

    ​ 一是要想对设计的算法的运行性能进行评测，需要实际运行该程序；

    ​ 二是所得时间的统计量依赖于计算机的硬件、软件等环境因素, 这种方式，要在同一台计算机的相同状态下运行，才能比较那个算法速度更快。

  2. 事前估算的方法
    通过分析某个算法的 时间复杂度来判断哪个算法更优.

1.3.2 时间频度

基本介绍

时间频度：一个算法花费的时间与算法中语句的执行次数成正比例，哪个算法中语句执行次数多，它花费时间
就多。 一个算法中的语句执行次数称为语句频度或时间频度。记为 T(n)。

比如计算 1-100 所有数字之和, 我们设计两种算法：

忽略常数项

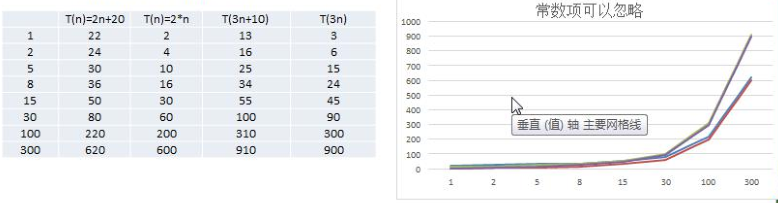
  • 2n+20 和 2n 随着 n 变大，执行曲线无限接近, 20 可以忽略
  • 3n+10 和 3n 随着 n 变大，执行曲线无限接近, 10 可以忽略
忽略低次项

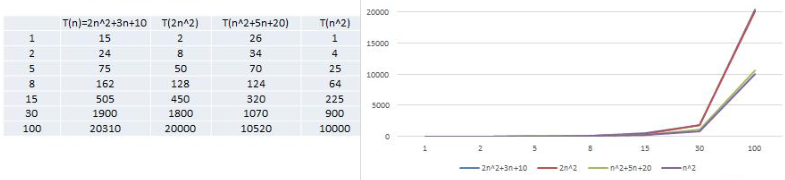
  • 2n^2+3n+10 和 2n^2 随着 n 变大, 执行曲线无限接近, 可以忽略 3n+10
  • n^2+5n+20 和 n^2 随着 n 变大,执行曲线无限接近, 可以忽略 5n+20
忽略系数

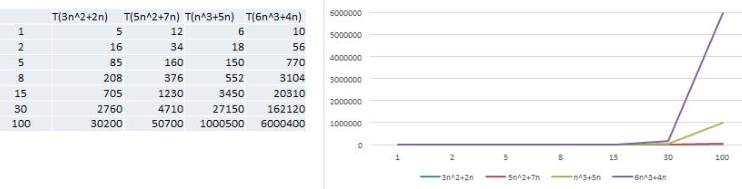
  • 随着 n 值变大，5n^2+7n 和 3n^2 + 2n ，执行曲线重合, 说明 这种情况下, 5 和 3 可以忽略。
  • 而 n^3+5n 和 6n^3+4n ，执行曲线分离，说明多少次方式关键

1.3.3 时间复杂度

  • 一般情况下， 算法中的基本操作语句的重复执行次数是问题规模 n 的某个函数，用 T(n)表示，若有某个辅
    助函数 f(n)，使得当 n 趋近于无穷大时，T(n) / f(n) 的极限值为不等于零的常数，则称 f(n)是 T(n)的同数量级函数。记作 T(n)= Ｏ( f(n) )，称Ｏ( f(n) ) 为算法的渐进时间复杂度，简称时间复杂度。
  • T(n) 不同，但时间复杂度可能相同。 如：T(n)=n²+7n+6 与 T(n)=3n²+2n+2 它们的 T(n) 不同，但时间复杂
    度相同，都为 O(n²)。
计算时间复杂度的方法
  • 用常数 1 代替运行时间中的所有加法常数 T(n)=n²+7n+6 => T(n)=n²+7n+1
  • 修改后的运行次数函数中，只保留最高阶项 T(n)=n²+7n+1 => T(n) = n²
  • 去除最高阶项的系数 T(n) = n² => T(n) = n² => O(n²)

1.3.4 常见的时间复杂度

  1. 常数阶 O(1)
  2. 对数阶 O(log2n)
  3. 线性阶 O(n)
  4. 线性对数阶 O(nlog2n)
  5. 平方阶 O(n^2)
  6. 立方阶 O(n^3)
  7. k 次方阶 O(n^k)
  8. 指数阶 O(2^n)
常见的时间复杂度对应的图

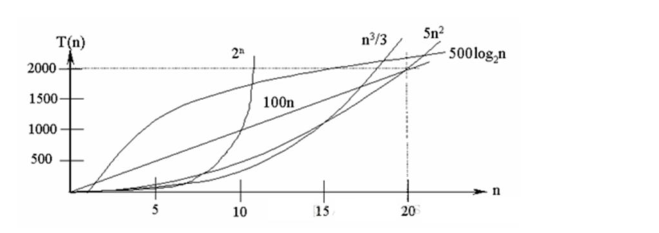
常见的算法时间复杂度由小到大依次为：``Ο(1)＜Ο(log2n)＜Ο(n)＜Ο(nlog2n)＜Ο(n2)＜Ο(n3)＜ Ο(nk) ＜ Ο(2n) ，随着问题规模 n 的不断增大，上述时间复杂度不断增大，算法的执行效率越低，从图中可见，我们应该尽可能避免使用指数阶的算法

常数阶 O(1)

对数阶 O(log2n)

线性阶 O(n)

线性对数阶 O(nlogN)

平方阶 O(n²)

立方阶 O(n³)、K 次方阶 O(n^k)

参考上面的 O(n²) 去理解就好了，O(n³)相当于三层 n 循环，其它的类似

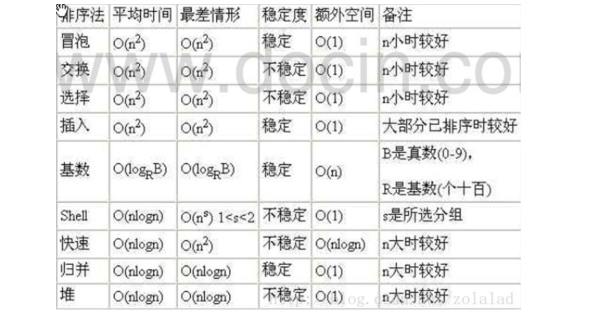
1.3.5 平均时间复杂度和最坏时间复杂度

  1. 平均时间复杂度是指所有可能的输入实例均以等概率出现的情况下，该算法的运行时间。
  2. 最坏情况下的时间复杂度称最坏时间复杂度。 一般讨论的时间复杂度均是最坏情况下的时间复杂度。这样做的
    原因是：最坏情况下的时间复杂度是算法在任何输入实例上运行时间的界限，这就保证了算法的运行时间不会
    比最坏情况更长。
  3. 平均时间复杂度和最坏时间复杂度是否一致，和算法有关(如图:)。

1.4 算法的空间复杂度简介

1.4.1基本介绍

  1. 类似于时间复杂度的讨论，一个算法的空间复杂度(Space Complexity)定义为该算法所耗费的存储空间，它也是
    问题规模 n 的函数。
  2. 空间复杂度(Space Complexity)是对一个算法在运行过程中临时占用存储空间大小的量度。有的算法需要占用的
    临时工作单元数与解决问题的规模 n 有关，它随着 n 的增大而增大，当 n 较大时，将占用较多的存储单元，例
    如快速排序和 归并排序算法, 基数排序就属于这种情况
  3. 在做算法分析时，主要讨论的是时间复杂度。 从用户使用体验上看 ， 更看重的程序执行的速度。一些缓存产品(redis, memcache)和算法(基数排序) 本质就是用空间换时间.