数据结构之栈Stack

栈的应用场景

  • 子程序的调用：在跳往子程序前，会先将下个指令的地址存到堆栈中，直到子程序执行完后再将地址取出，以
    回到原来的程序中。
  • 处理递归调用：和子程序的调用类似，只是除了储存下一个指令的地址外，也将参数、区域变量等数据存入堆
    栈中。
  • 表达式的转换[中缀表达式转后缀表达式]与求值(实际解决)。
  • 二叉树的遍历。
  • 图形的深度优先(depth 一 first)搜索法。

1. 栈入门

  • 栈是一个 先入后出(FILO-First In Last Out) 的有序列表。
  • 栈(stack) 是限制线性表中元素的插入和删除只能在线性表的同一端进行的一种特殊线性表。 。 允许插入和删除的一端，为 变化的一端，称为栈顶(Top) ，另一端为 固定的一端，称为栈底(Bottom) 。
  • 根据栈的定义可知 ， 最先放入栈中元素在栈底 ， 最后放入的元素在栈顶 ， 而删除元素刚好相反 ， 最后放入的元素最先删除，最先放入的元素最后删除
  • 图解方式说明出栈(pop) 和入栈(push)

1.1 使用数组模拟栈

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
/**
 * @author DuanChaojie
 * @date 2020年2月24日 下午7:23:10
 * @version 1.0
 * 通过数组定义的栈
 */
class ArrayStack{
	
	//栈的最大容量
	private int maxSize;

	//来装数据
	private int[] stack;
	
	//栈顶,初始化为-1
	private int top = -1;
	
	//构造器，初始化栈
	public ArrayStack(int maxSize) {
		this.maxSize = maxSize;
		stack = new int[maxSize];
	}
	
	//判断栈是否满
	public boolean isFull() {
		return top == maxSize - 1;
	}
	
	//判断栈是否空
	public boolean isEmpty() {
		return top == -1;
	}
	
	//入栈的方法push
	public void push(int value) {
		//先判断栈是否满
		if(isFull()) {
			System.out.println("栈满，不能push数据");
			return;
		}
		
		top++;
		stack[top] = value;
	}
	
	//出栈的方法pop
	public int pop() {
		if(isEmpty()) {
			/**
			 * 	System.out.println("栈空，不能pop数据");
			 *  return;
			 *  因为该方法的返回值为int所以不能通过return;来结束该方法，所以选择抛出一个异常
			 */
			throw new RuntimeException("栈空，不能pop数据");
		}
		int temp = stack[top];
		top--;
		return temp;
	}
	
	
	//遍历栈方法showList,从栈顶显示数据
	public void showList() {
		
		if(isEmpty()) {
			System.out.println("栈空，不能遍历数据");
			return;
		}
		
		for(int i = top;i>=0;i--) {
			System.out.printf("stack[%d]=%d\n",i,stack[i]);
		}
	}	
}

1.2 测试栈

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
class ArrayStackDemo {

	public static void main(String[] args) {
		//初始化栈
		ArrayStack stack = new ArrayStack(4);
		
		Scanner scanner = new Scanner(System.in);
		
		boolean flag = true;
		
		String key = "";
		
		while(flag) {
			System.out.println("show:表示显示程序");
			System.out.println("push:表示添加数据到栈");
			System.out.println("pop:表示取出栈中的数据");
			System.out.println("exit:表示退出程序");
			System.out.println("请您输入要执行程序的指令...");
			
			key = scanner.next();
		
			switch (key) {
			case "show":
				stack.showList();
				break;
			case "push":
				System.out.println("请输入一个数添加到stack栈中");
				int result = scanner.nextInt();
				stack.push(result);
				break;
			case "pop":
				stack.pop();
				break;
			case "exit":
				scanner.close();
				flag = false;
				break;
			default:
				break;
			}
		}
		System.out.println("程序退出！");

	}

}

2. 栈实现综合计算器(中缀表达式)

2.1 思路分析图

2.2 创建栈（添加一些方法）

增加的方法：

  • public int peek();可以返回当前栈顶的值，但不是真正的pop
  • public int priority(int oper);返回运算符的优先级
  • public boolean isOper(char val);判断是不是一个运算符
  • public int cal(int num1,int num2,int oper);计算方法
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
/*
 * 先创建一个栈，使用前面的，修改一下
 * */
class ArrayStack2{
	
	//栈的最大容量
	private int maxSize;

	//来装数据
	private int[] stack;
	
	//栈顶,初始化为-1
	private int top = -1;
	
	//构造器，初始化栈
	public ArrayStack2(int maxSize) {
		this.maxSize = maxSize;
		stack = new int[maxSize];
	}
	
	//判断栈是否满
	public boolean isFull() {
		return top == maxSize - 1;
	}
	
	//判断栈是否空
	public boolean isEmpty() {
		return top == -1;
	}
	
	//增加一个方法，可以返回当前栈顶的值，但不是真正的pop
	public int peek() {
		return stack[top];
	}
	

	
	
	//入栈的方法push
	public void push(int value) {
		//先判断栈是否满
		if(isFull()) {
			System.out.println("栈满，不能push数据");
			return;
		}
		
		top++;
		stack[top] = value;
	}
	
	//出栈的方法pop
	public int pop() {
		if(isEmpty()) {
			/**
			 * 	System.out.println("栈空，不能pop数据");
			 *  return;
			 *  因为该方法的返回值为int所以不能通过return;来结束该方法，所以选择抛出一个异常
			 */
			throw new RuntimeException("栈空，不能pop数据");
		}
		int temp = stack[top];
		top--;
		return temp;
	}
	
	
	//遍历栈方法showList,从栈顶显示数据
	public void showList() {
		
		if(isEmpty()) {
			System.out.println("栈空，不能遍历数据");
			return;
		}
		
		for(int i = top;i>=0;i--) {
			System.out.printf("stack[%d]=%d\n",i,stack[i]);
		}
	}
	
	//扩展的功能：返回运算符的优先级，由程序员定的使用数字表示
	//数字越大，优先级越高
	public int priority(int oper) {
		if(oper == '*' || oper == '/') {
			return 1;
		}else if(oper == '+' || oper == '-') {
			return 0;
		}else {
			//假定目前表达式只有  + - * /
			return -1;
		}
		
	}
	
	//判断是不是一个运算符
	public boolean isOper(char val) {
		return val == '+' || val == '-' || val == '*' || val == '/';
	}
	
	//计算方法
	public int cal(int num1,int num2,int oper) {
		//res用于存放计算的结果
		int res = 0;
		
		switch (oper) {
		case '+':
			res = num1+num2;
			break;
		case '-':
			res = num1-num2;
			break;
		case '*':
			res = num1*num2;
			break;
		case '/':
			res = num1/num2;
			break;
		default:
			break;
		}
		
		return res;
	}

2.3 栈实现综合计算机–逻辑

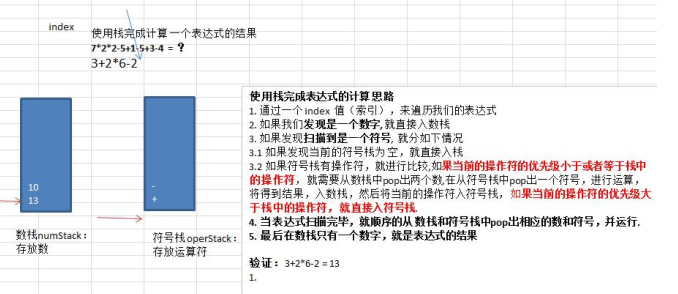
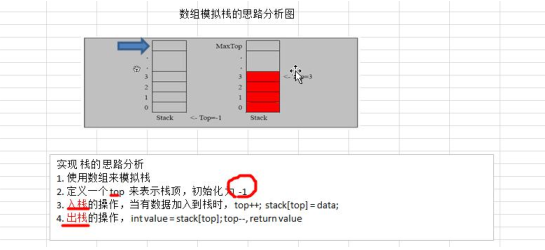
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
public class Calculator {

	public static void main(String[] args) {
		
		//计算机传来的字符串
		String expression = "300+2*2*2-1";
		
		//需要先创建numStack和operStack
		ArrayStack2 numStack = new ArrayStack2(10);
		ArrayStack2 operStack = new ArrayStack2(10);
		
		int index = 0;//用于扫描
		int num1 = 0;
		int num2 = 0;
		int oper = 0;
		int res = 0;
		char ch = ' ';//将每次扫描得到的char保存到ch
		String keepNum = "";//用于拼接多位数
		
		//开始while循环通过index扫描expreesion
		while(true) {
		
			//得到扫描得到的字符
			ch = expression.substring(index,index+1).charAt(0);
			
			//判断ch是什么，然后做出相应的处理
			if(index == 0 && operStack.isOper(ch)) {
				throw new RuntimeException("表达式不规范");
			}
			
			//如果是运算符
			if(operStack.isOper(ch)) {
				if(!operStack.isEmpty()) {
					if(operStack.priority(operStack.peek())>=operStack.priority(ch)) {
						num2 = numStack.pop();
						num1 = numStack.pop();
						oper = operStack.pop();
						res = numStack.cal(num1, num2, oper);
						numStack.push(res);
						index--;
					}else {
						operStack.push(ch);
					}
				}else {
					operStack.push(ch);
				}
				
			}else {
				//如果是数字，直接入数栈
				//numStack.push(ch-48);
				//处理多位数
				keepNum +=ch;
				
				//判断下一个字符是不是数字，如果是数字，就继续扫描，如果是运算符，则入栈
				//注意是看后一位，不是index++
				if(index == expression.length()-1) {
					numStack.push(Integer.parseInt(keepNum));
				}else {
						if(operStack.isOper(expression.substring(index+1,index+2).charAt(0))) {
							numStack.push(Integer.parseInt(keepNum));
							//keepNum一定要清空，不然会影响后面的计算
							keepNum = "";		
						}					
				}
				
			
			}
			/**测试片段
			System.out.println("numStack");
			numStack.showList();
			System.out.println("operStack");
			operStack.showList();
			 */
	
			index++;
			//判定循环结束
			if(index>=expression.length()) {	
				break;
			}
			
		}
		
		while(true) {
		
			if(operStack.isEmpty()) {
				break;
			}
			num2 = numStack.pop();
			num1 = numStack.pop();
			oper = operStack.pop();
			res = numStack.cal(num1, num2, oper);
			numStack.push(res);
			
		}
		
		int pop = numStack.pop();
		System.out.println(pop);
		System.out.printf("计算: %s = %d",expression,pop);
		

	}

3. 栈实现综合计算器（后缀表达式）

3.1 逆波兰表达式的计算

  • public static List<String> getListString(String suffixExpression);将一个逆波兰表达式，依次将数据和运算符放入到ArrayList中。
  • public static int calculate(List<String> ls);完成逆波兰表达式的运算 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
public class PolandNotation {

	public static void main(String[] args) {
	
	}
	
	/**
	 * 将一个逆波兰表达式，依次将数据和运算符放入到ArrayList中
	 * */
	public static List<String> getListString(String suffixExpression){
		String[] split = suffixExpression.split(" ");
		ArrayList<String> list = new ArrayList<String>();
		for (String ele : split) {
			list.add(ele);
		}
		return list;
	}
	
	
	/**
	 * 完成逆波兰表达式的运算 
	* */
	public static int calculate(List<String> ls) {
		//创建栈，只需要一个栈即可
		Stack<String> stack = new Stack<String>();
		
		//遍历逆波兰表达式
		for (String item : ls) {
			//这里使用正则表达式运算
			if(item.matches("\\d+")) {//匹配的是多位数
				//入栈
				stack.push(item);
			}else {
				
				int num2 = Integer.parseInt(stack.pop());
				int num1 = Integer.parseInt(stack.pop());
				
				int res = 0;
				//进行运算
				if(item.equals("+")) {
					res = num1 + num2;
				}else if(item.equals("-")) {
					res = num1 - num2;
				}else if(item.equals("*")) {
					res = num1 * num2;
				}else if(item.equals("/")) {
					res = num1 / num2;
				}else {
					throw new RuntimeException("运算符有误！");
				}
				//把res入栈
				stack.push(""+res);
			}
			
		}
		//最后留在stack中的就是运算结果
		return Integer.parseInt(stack.pop());
	}
}

3.2 中缀表达式转后缀表达式

  • class Operation的getValue();返回一个运算符对应的优先级.
  • public static List<String> toInfixExpressionList(String s);将中缀表达式转成List。
  • public static List<String> parseSuffixExpressionList(List<String> ls);将得到的中缀表达式对应的list转成后缀表达式list
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
public class PolandNotation {

	public static void main(String[] args) {
	}
	


	/**
	 * 将中缀表达式转成List
	 */
	public static List<String> toInfixExpressionList(String s){
		//定义一个list存放中缀表达式对应的内容
		List<String> ls = new ArrayList<String>();
		//这是一个指针，用于遍历中缀表达式字符串
		int i = 0;
		//多位数的拼接
		String str;
		//每遍历到一个字符，就放到c
		char c;
		do {
			//如果c是一个非数字，我需要加入到ls
			if((c=s.charAt(i))<48 || (c=s.charAt(i))>57) {
				ls.add(""+c);
				//i需要后移
				i++;
			}else {
				//如果是数，需要考虑多位数
				str = "";
				
				while(i<s.length() && (c=s.charAt(i))>=48 && (c=s.charAt(i))<=57) {
					str +=c;//拼接
					i++;
				}
				ls.add(str);
			}
			
				
			
		}while(i<s.length());
		
		return ls;//返回
	}
	
	
	/***
	 * 将得到的中缀表达式对应的list转成后缀表达式list
	 */
	public static List<String> parseSuffixExpressionList(List<String> ls){
		//定义一个栈一个List
		Stack<String> s1 = new Stack<String>();//符号栈
		
		List<String> s2 = new ArrayList<String>();//储存中间的结果s2
		
		//遍历ls
		for (String item : ls) {
			
			//如果是一个数，加入到s2
			if(item.matches("\\d+")) {
				
				s2.add(item);
			}else if(item.equals("(")) {
				
				s1.push(item);
			}else if(item.equals(")")) {
				
				//如果是右括号“）” 则依次弹出s1栈顶的运算符，
				//并压入s2,直到遇到左括号为止，此时将这一对括号丢弃
				while(!s1.peek().equals("(")) {
					s2.add(s1.pop());
				}
				
				//将 （  弹出s1,消除小括号
				s1.pop();
				
			}else {
				//当item的优先级小于等于s1栈顶的运算符，将s1栈顶的运算符弹出并加入到s2
				while(s1.size()!=0 && Operation.getValue(s1.peek())>=Operation.getValue(item)) {
					s2.add(s1.pop());
				}
				s1.push(item);
				
				
			}
		}
		
		//将s1中剩余的运算符依次弹出并加入s2
		while(s1.size()!=0) {
			s2.add(s1.pop());
		}
		
		//注意因为是存放到List 因此按顺序输出就是对应的后缀表达式的List
		return s2;
		
	}
	
	
	
}

/**
 * 返回一个运算符对应的优先级
 * @author DuanChaojie
 * @date 2020年2月27日 下午8:39:51
 * @version 1.0
 */
class Operation{
	private static int ADD = 1;
	private static int SUB = 1;
	private static int MUL = 2;
	private static int DIV = 2;
	
	//返回对应的优先级数字
	public static int getValue(String operation) {
		int result = 0;
		
		switch (operation) {
		case "+":
			result = ADD;
			break;
		case "-":
			result = SUB;
			break;
		case "*":
			result = MUL;
			break;
		case "/":
			result = DIV;
			break;
		default:
			System.out.println("不存在该运算符");
			break;
		}
		return result;
	}
	
}

3.3 测试逆波兰计算器

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
public class PolandNotation {

	public static void main(String[] args) {
		//将中缀表达式转变成后缀表达式
		String expression = "1+((2+3)*4)-5";
		List<String> list = toInfixExpressionList(expression);
		System.out.println("List="+list);
		List<String> parseSuffixExpressionList = parseSuffixExpressionList(list);
		System.out.println("后缀表达式："+parseSuffixExpressionList);
		
		String suffixExpression = "";
		for (String string : parseSuffixExpressionList) {
			 suffixExpression += " "+ string;
			 System.out.println(suffixExpression);
		}
		
		/**
		 * 思路：
		 * 	1.先将 "3 4 + 5 * 6 -" 放入到一个ArrayList中
		 *  2.将ArrayList传递给一个方法，遍历ArrayList 配合栈完成计算
		 *  3.添加测试 4*5-8+60+8/2 --> 4 5 * 8 - 60 + 8  2 / +   -->76
		 */
		
		//先定义一个逆波兰表达式
		//说明为了方便，逆波兰表达式的数字和符号使用空格隔开
		//String suffixExpression = "4 5 * 8 - 60 + 8 2 / +";
		
		List<String> rpnList = getListString(suffixExpression.substring(1));
		System.out.println("rpnList："+rpnList);
		int result = calculate(rpnList);
		System.out.println("运算的结果是："+result);
		
		
	}
}